
WRD-PLT (Word Plate) is a game we play on road trips. The game is simple: as another car drives by, take the three letters on their license plate, and come up with words containing all three letters in that order.
But not all three-letter triplets are fun for this game. Some are impossible ("ZQX"). Some are too easy ("ING"). Here we apply statistical analysis to come up with a set of triplets that are within the goldilocks zone of playability.
And you can play the game at https://wrd-plt.ovisly.com/!
At Ovisly, we have unofficial Friday hackathons once in a while. This time, I thought I'd investigate a little game I like to play while driving.
Many states in the US have license plate formats containing three consecutive letters, plus three or four digits. For example, ABC-123, ABC-1234, or 1ABC234 . So driving on the road, we see a lot of cars with an assortment of three-letter combinations. The game is to come up with words that contain all three letters in that order.
For example, if a car with the license plate "UIY 123" drives by, acceptable answers are "unity", "quality", or even "immunohistochemistry", and many more. The longer the word, the better!
For some letter triplets, the ideas are flowing and we'd be shouting words back and forth. But some letter triplets are quite difficult that I just draw a blank. If I see a car with the license plate of "XXG 123", I won't even try because I don't think there's any word that would contain X, X, and G. On the other hand, if there's another car with "ING 123", then we also wouldn't start a new round becase there are just too many words with I, N, and G. It'd need to be a very very long drive to name all the present participles.
So there's a sweet spot of difficulty level that makes some three-letter triplets more fun to play. Then, how do we pick these goldilocks triplets that are not impossibly difficult, yet at the same time not too easy to be boring?
A Statistical Analysis of All Three-Letter Triplets
There are 26 x 26 x 26 = 17,576 possible three-letter triplets. For now we are ignoring the fact that not all letters are used in license plates, such as I and O (more information here).
We also need a source of all English words. For this exercise we went with the wordfreq python library.
Then, for each of the 17,576 three-letter triplets, we check against the list of English words to see how many possible answers each triplet has.
"""Survey all three-letter triplets to see distribution."""
import re
import pickle
import string
from tqdm import tqdm
from wordfreq import iter_wordlist, zipf_frequency
CHAR_SET = string.ascii_letters
CHAR_SET_LOWER = string.ascii_lowercase
def has_only_latin_letters(input_string):
"""Check if input string contains only ascii letters."""
return all((True if x in CHAR_SET else False for x in input_string))
def make_cleaned_wordlist():
"""Parse wordlist to include only those with letters."""
return [
word for word in iter_wordlist('en', wordlist='large')
if has_only_latin_letters(word)
]
def letters_in_word(list_letters, word):
"""Check if a list of letters are in a word in the given order."""
pattern = "[a-z]*" + "+[a-z]*".join(list_letters) + "+[a-z]*"
return bool(re.match(pattern, word))
if __name__ == '__main__':
wordlist = make_cleaned_wordlist()
list_letters_all = [
[i, j, k]
for i in CHAR_SET_LOWER for j in CHAR_SET_LOWER for k in CHAR_SET_LOWER
]
dict_out = {}
for list_letters in tqdm(list_letters_all):
list_words_with_letters = [
(word, zipf_frequency(word, "en", wordlist="large"))
for word in wordlist if letters_in_word(list_letters, word)
]
dict_out["".join(list_letters)] = list_words_with_letters
with open("./output/output.pkl", "wb") as outfile:
pickle.dump(dict_out, outfile, pickle.HIGHEST_PROTOCOL)
With this result, we can look up any three-letter triplet and get the list of all valid answers.
Word Frequency
The result is structured as a dictionary keyed on the three-letter triplet. For each triplet, we can look up all the valid words. In addition, we are outputting the Zipf frequency from the wordfreq library.
Zipf frequency of a word is very informative. It's the frequency of occurrence of a word on the log scale (which is much easier to digest than the raw frequency - a very very small number).
For example, let's look up what words can be made from the triplet ZZZ. I can't think of any. But looking up the dictionary, we see:
>>> dict_results["zzz"]
[('pizzazz', 2.28),
('zzz', 2.21),
('zazzle', 2.04),
('pizazz', 1.85),
('razzmatazz', 1.84),
('zzzz', 1.8),
('zzzzz', 1.49),
('bzzz', 1.45),
('zzzzzz', 1.37),
('zzyzx', 1.36),
('zizzi', 1.34),
('zzzzzzz', 1.29),
('zazz', 1.25),
('zizzo', 1.25),
('pizzaz', 1.24),
('buzzz', 1.22),
('zyzz', 1.22),
('plzzz', 1.13),
('zaporizhzhya', 1.13),
('zzzs', 1.13),
('bzzzz', 1.11),
('zzzzzzzz', 1.1),
('razzamatazz', 1.05),
('zzzquil', 1.04),
('azzouz', 1.02)]
Ok, I should've thought of "pizzazz" and "zazzle". I have heard of "razzmatazz". But this is my first time learning about "zaporizhzhya", and there are words that aren't really English words, like "plzzz". Can't get points from Scrabble with this one.
That's because wordfreq library learns words from many sources: Wikipedia, news, books, Twitter, and many more. So it represents words that people use. Now that I think of it, I probably have typed "plzzz" at some point in my life.
And just for fun, we can see the Zipf frequency for the a's and z's. This table also gives us a bit of intuition on the relationship between Zipf frequency values and how "common" and "familiar" and "easy to recall" a word is.
"word" | Zipf Frequency
----------------------------
a | 7.36
aa | 4.01
aaa | 3.77
aaaa | 2.59
aaaaa | 2.04
aaaaaa | 1.74
aaaaaaa | 1.45
aaaaaaaa | 1.34
aaaaaaaaa | 1.27
aaaaaaaaaa | 1.13
|
z | 4.47
zz | 2.8
zzz | 2.21
zzzz | 1.8
zzzzz | 1.49
zzzzzz | 1.37
zzzzzzz | 1.29
zzzzzzzz | 1.1
Quantifying Difficulty
For a three-letter triplet, it's easier to think of words if there are many words that contain these letters.
So we can iterate through the triplet dictionary to count how many words each triplet has. We can also count total points: each word's number of points is its number of letters. So that we reward players for coming up with longer words.
Doing so allows us to rank the triplets by the number of possible answers. The higher a triplet ranks, the "easier" it is to come up with words. We also see that out of 17,576 possible triplets, only 525 (3%) do not have any valid answers.
Let's see what a middle-of-the-pack triplet look like. The exact middle of the ranking sits the letters "YEV". What words are made of "YEV"? I'm drawing blank again. But we do have the answers:
>>> dict_results["yev"]
[('yourselves', 3.86),
('fayetteville', 3.04),
('hyperactivity', 2.86),
('hypersensitivity', 2.77),
('hyperactive', 2.76),
('yeovil', 2.72),
('yerevan', 2.7),
('yeshiva', 2.67),
('hyperventilating', 2.54),
('hypertensive', 2.49),
...
...
('cyberverse', 1.01),
('flyleaves', 1.01),
('grigoryev', 1.01),
('hypergravity', 1.01),
('jayadev', 1.01),
('yakushev', 1.01),
('yevon', 1.01)]
Ok, maybe I should've come up with "yourselves", but "hypersensitivity"? I don't feel too disappointed in myself that I didn't see "YEV" and think of "hypersensitivity".
Our observations so far provide us with some intuitions about how to measure difficulty of each triplet:
- Easier triplets have more valid answers
- Easier triplets have answers that are easier words
- Easier words have higher Zipf frequency
- Easier words are shorter
Difficulty Distribution
Based on the "difficulty metrics" above, we select the triplets based on a heuristics: triplets that have a total of at least 150 points from words that are not too difficult, namely, they have a Zipf frequency of greater or equal to 2.5 and word length less or equal to 7 characters.
With this condition, we have now reduced the triplets from 17,576 down to 4,402 (25%). And here are the highest ranked triplets, representing the easiest ones, which are probably too easy to be fun.
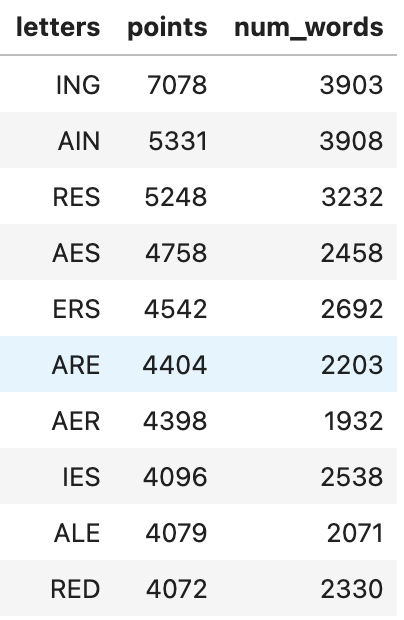
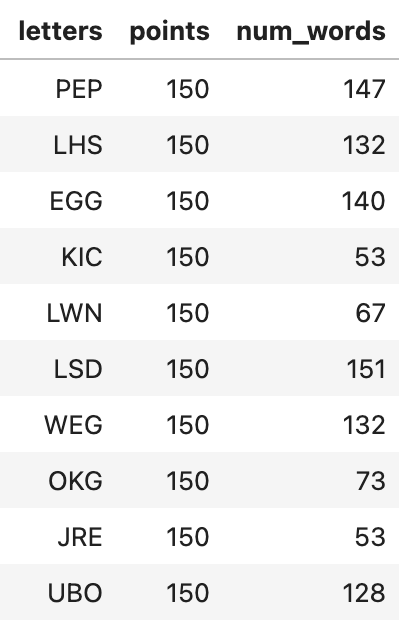
And here are the triplets at the bottom of the list of 4,402. They are the most difficult triplets, but should still be doable given the selection criteria we have imposed.
If we plot the distribution of number of words possible for each triplet, we see that there is a long tail. The top triplet, "ING", has nearly 4k possible answers (and we are only counting the "common" ones with high enough Zipf frequency).
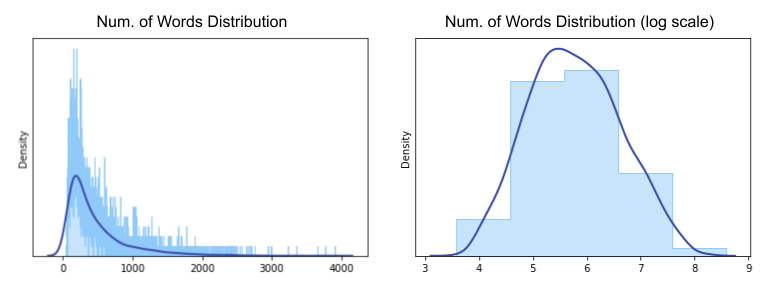
Defining the Playable Zone
The left-hand side of the distribution represents more difficult triplets. We have already trimmed this end by imposing conditions on Zipf frequency and word length. The right-hand side of the distribution represents triplets that are too easy. We do need to trim this side significantly so the game can be challenging.
We decided to go with a simple percentile cut: remove the top 25 percent easiest triplets. We also trimmed around 10 percent from the left side, just to reduce even further the more difficult triplets. That leaves us with 2,832 triplets.
So out of 17,576 possible triplets, we have selected 2,832 (16%) as playable.
The Game
But is it really fun now that we have a set of "ideal" triplets? You can decide! We have set up the game at https://wrd-plt.ovisly.com/. Each round, a random triplet is drawn from the 2,832 pool, and you can type as many words as you can think of. Each word is worth as many points as its length. Enjoy!

Above: A screenshot of the WRD PLT game that you can play at https://wrd-plt.ovisly.com/.
